НиД (10) - Лекция №3 - Расчёт невосстанавливаемых систем

Показатели надёжности невосстанавливаемых систем

Большинство систем описывается характеристиками простейших потоков.

$$\lambda$$ - инденсивность отказов, количество отказов в единицу времени.

Если $$\lambda\cdot\Delta t << 1$$, то $$e^{-\lambda\cdot\Delta t}\approx 1 - \lambda\cdot\Delta t$$

$$m_t = M[T]$$

$$m_t = \int_0^\infty P(t)dt$$

если $$\lambda = const$$, то $$m_t = \frac{1}{\lambda}$$ - мат.ожидание времени наработки на отказ.

Методы расчёта надёжности невосстанавливаемых систем

Последовательные схемы

$$P_p = e^{-\lambda_1 t}\cdot e^{-\lambda_2 t}$$

$$\lambda_p = \lambda_1 + \lambda_2$$

$$\lambda_1 = \frac{1}{T_1}$$

$$\lambda_2 = \frac{1}{T_2}$$

$$T_p = \frac{1}{\lambda_p} = \frac{T_1\cdot T_2}{T_1 + T_2}$$

Параллельные схемы

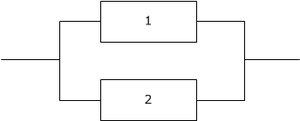
$$P_p = P_1 + P_2 - P_1\cdot P_2$$ - вероятность исправной работы.

$$R_p = 1 - P_p$$ - вероятность отказа.

$$T_p = \int_0^\infty P(t)dt$$

Если имеется система параллельно включённых элементов, какждый из которых описывается экспоненциальным законом, то результирующий закон системы точно не является экспоненциальным (простейшим) - есть небольшое отличие.

Время наработки на отказ системы из разных элементов: $$T = (\frac{1}{\lambda_1} + \frac{1}{\lambda_2} + ... + \frac{1}{\lambda_n}) - (\frac{1}{\lambda_1 + \lambda_2} + \frac{1}{\lambda_1 + \lambda_3} + ...) - ... + (-1)^{n+1}\frac{1}{\sum_{i=1}^n \lambda_i}$$

Время наработки на отказ системы из одинаковых элементов: $$T_p = \frac{1}{\lambda}\cdot\sum_{i=0}^n\frac{1}{i}$$

Пример для параллельных

Работают два двигателя самолёта (один - горячий резерв). Если один выходит из строя, то система ещё работает. Какова вероятность безотказной работы $$P$$ в течение 400 часов. Интенсивность отказа каждого двигателя $$\lambda = 0.0005$$, отказы происходят статистически независимо.

$$P(400) = 2\cdot e^{-0.0005\cdot 400} - e^{-2\cdot 0.0005\cdot 400} = 0.9671$$

Из 100 самолётов за 400 часов упадёт 4.

Среднее время наработки на отказ: $$T_p = \frac{1}{\lambda}\cdot (1 + \frac{1}{2} = 3000$$ часов.

Топологически сложные схемы

Метод разрезания по ключевому элементу

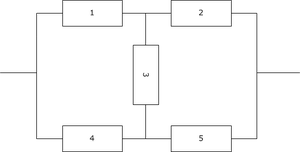
На примере мостиковой схемы:

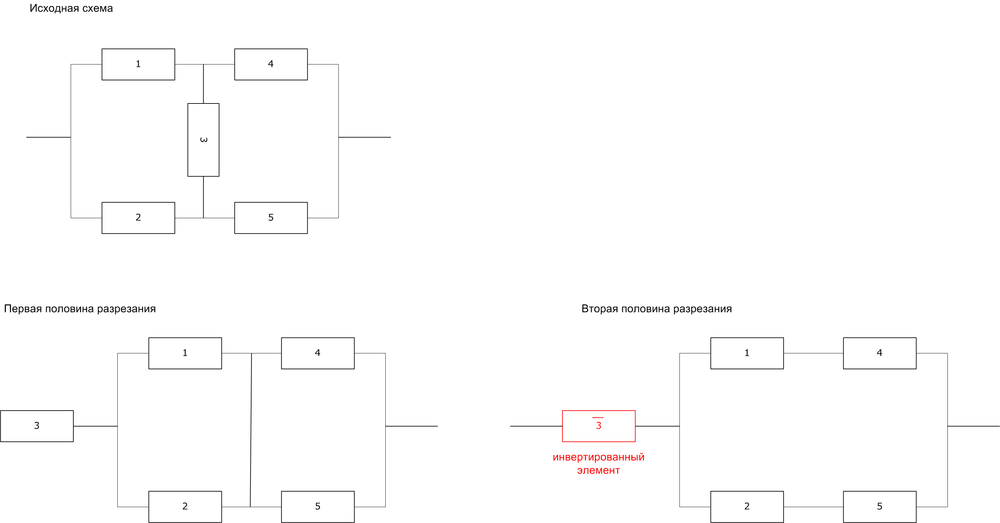
Вероятность безотказной работы исходной схемы равна сумме вероятностей безотказных работ схем, на которые мы разрезали исходную.

И есть готовая формула для такой:

$$P_p = 2\cdot P_1\cdot P_2\cdot P_3\cdot P_4\cdot P_5 - P_2\cdot P_3\cdot P_4\cdot P_5 - P_1\cdot P_3\cdot P_4\cdot P_5 - P_1\cdot P_3\cdot P_5 - ...$$ $$+ P_1\cdot P_3\cdot P_5 + P_2\cdot P_3\cdot P_4 + P_1\cdot P_4 + P_2\cdot P_5$$

$$P_p = 2\cdot P^5 - 5\cdot P^4 + 2\cdot P^3 + 2\cdot P^2$$

$$P(t) = 2\cdot e^{-5\cdot\lambda t} - 5\cdot e^{-4\cdot\lambda t} + 2\cdot e^{-3\cdot\lambda t} + 2\cdot e^{-2\cdot\lambda t}$$

$$T_p = \frac{49}{60}\cdot\frac{1}{\lambda}$$

Пример

Определить вероятность безотказной работы мостиковой системы и среднее время наработки на отказ для случая $$\lambda = 0.0005$$, $$T = 100$$.

$$P(t) = 2\cdot e^{-5\cdot\lambda t} - 5\cdot e^{-4\cdot\lambda t} + 2\cdot e^{-3\cdot\lambda t} + 2\cdot e^{-2\cdot\lambda t} = 0.9999$$

$$T_p = \frac{49}{60}\cdot\frac{1}{0.0005} = 1633.4$$

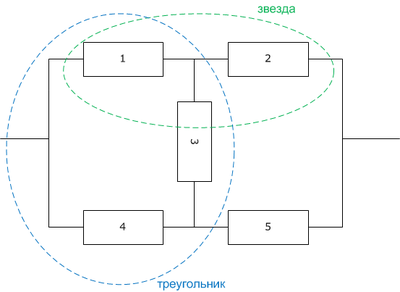
Метод преобразования треугольника в звезду и наоборот

Исходная и эквивалентная схемы:

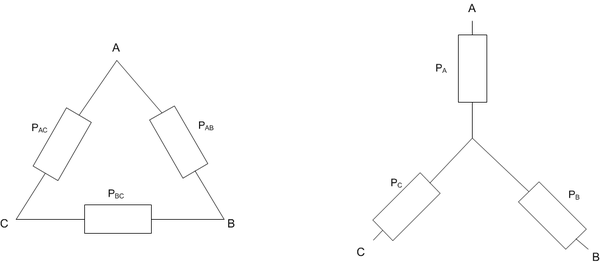
$$$P_A\cdot P_B = 1 - (1 - P_{AB})\cdot (1 - P_{AC}\cdot P_{CB})$$$

$$$P_A = \sqrt{\frac{(1 - (1 - P_{AC})\cdot (1 - P_{CB}\cdot P_{AB}))\cdot (1 - (1 - P_{AB})\cdot (1 - P_{AC}\cdot P_{CB}))}{1 - (1 - P_{CB})\cdot (1 - P_{AC}\cdot P_{AB})} } $$$

$$$P_B = \sqrt{\frac{(1 - (1 - P_{CB})\cdot (1 - P_{AC}\cdot P_{AB}))\cdot (1 - (1 - P_{AB})\cdot (1 - P_{AC}\cdot P_{CB}))}{1 - (1 - P_{AC})\cdot (1 - P_{CB}\cdot P_{AB})} } $$$

$$$P_C = \sqrt{\frac{(1 - (1 - P_{AC})\cdot (1 - P_{CB}\cdot P_{AB}))\cdot (1 - (1 - P_{CB})\cdot (1 - P_{AC}\cdot P_{AB}))}{1 - (1 - P_{AB})\cdot (1 - P_{AC}\cdot P_{CB})} } $$$

Метод путей и сечений

Он же метод минимальных путей и минимальных сечений. Приближённый.